Exploring High School Algebra: Finding the Circle's Center
Written on
Chapter 1: Understanding the Problem
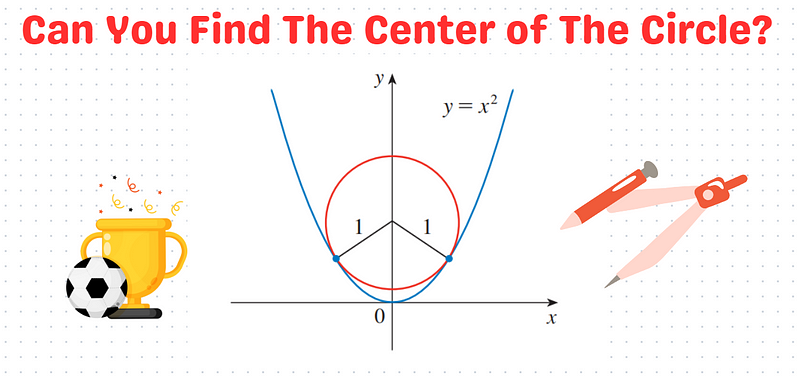
Let’s revisit high school algebra and tackle a fascinating problem. We have a circle with a radius of 1 that is inscribed within the parabola defined by the equation y = x². Can you determine the location of the circle's center?
Here’s a hint: the circle is tangent to the parabola and…
Take a moment to pause this article, grab your pencil and paper, and try to solve it. When you’re ready, continue reading for the solution!
Solution
We know the circle is positioned along the y-axis, which tells us the x-coordinate is 0. Our goal now is to find the y-coordinate, which we will denote as 'a'.
Recall from our algebra lessons that the equation x² + y² = r² represents a circle with a radius 'r' centered at the origin. Since our circle is located at (0, a), we can apply transformation techniques to derive its equation.

Our approach will leverage the fact that the circle is tangent to the parabola. This means we can substitute y = x² into the equation of the circle.
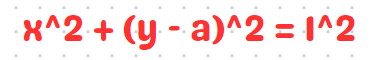
Let’s rearrange the resulting equation.
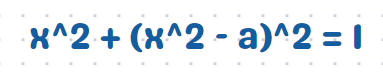
This manipulation leads us to a quadratic equation in terms of x². Did you notice the emoji in my hint? It actually signifies the discriminant!
The circle and parabola will be tangent when this quadratic equation has equal roots, which occurs when the discriminant equals zero. The discriminant of the quadratic equation ax² + bx + c is represented by b² - 4ac.
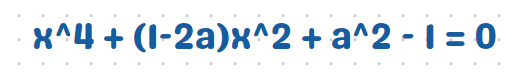
We are left to perform some basic algebraic manipulations. The terms involving 4a² cancel out, leading us to find that a = 5/4.

And that concludes our solution!
Isn’t it fascinating?
What were your thoughts during this process? I’d love to hear your insights in the comments below!
Chapter 2: Engaging with Math Puzzles
Discover a collection of the best math puzzles available on Medium, including topics like Algebra, Geometry, Calculus, and Number Theory. Share these challenges with your friends!
Thank you for taking the time to read this. If you found this article valuable, please consider giving it a clap!

If you enjoyed this content, and feel generous, consider buying me a coffee! Your support helps me continue writing and thriving in my personal and academic journey.
Happy Solving, Bella