Chapter 1: Introduction to Advanced Mathematical Concepts

Have you ever considered how to best challenge your top mathematics students? Reflecting on my own high school experiences, I recognized that many math lessons tend to be delivered in a repetitive and formulaic manner. Students often learn specific approaches and formulas for various problems, practicing them until they feel confident enough to tackle similar questions on tests.

However, simply learning to solve formulaic problems does not guarantee a deep understanding of the underlying concepts. Without this comprehension, students may struggle to apply their knowledge in new or unfamiliar contexts. To cultivate exceptional mathematicians, it's crucial to encourage them to think critically and adapt their knowledge to different situations. This leads to my exploration of teaching integration by parts in a way that transcends mere formula memorization.

Section 1.1: The Concept of Integration by Parts

Integration by parts is a fundamental technique taught in high school mathematics, designed for integrating the products of functions. Given a function v(x) and the derivative du/dx of another function u(x), this method allows us to compute the integral of their product.

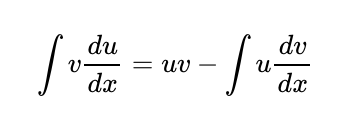
For instance, consider the integral of y = x * cos(x). If we set v = x and du/dx = cos(x), our integration by parts formula gives us:

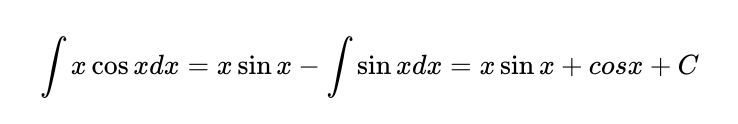
While the formula for integration by parts can be derived from the product rule of derivatives, my understanding of it has often been limited to rote memorization. In this discussion, I aim to unveil some intriguing geometric interpretations of this formula, which I believe will foster a deeper understanding of its significance.

Section 1.2: Visualizing Integration by Parts

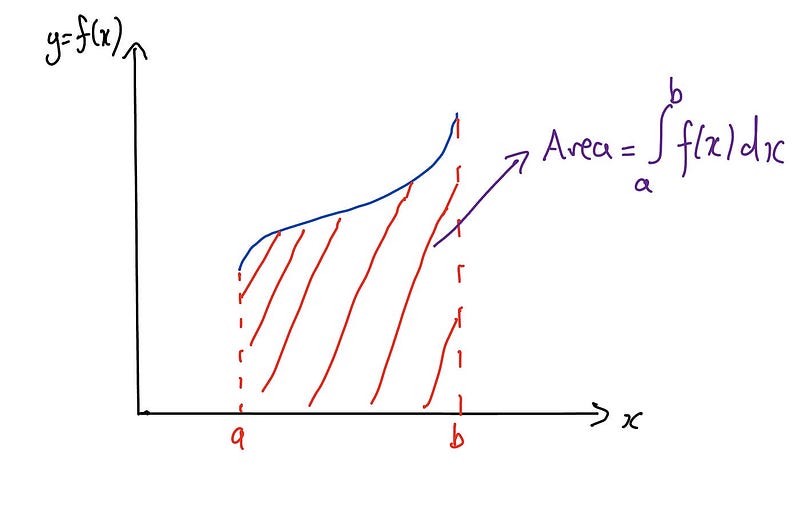
To visualize integration, imagine we have a function f(x) and wish to integrate it from x = a to x = b. For simplicity, let’s focus on the first quadrant of the Cartesian plane, where 0 ≤ a < b, and suppose that f(x) is a positive, continuous, and increasing function. Geometrically, integrating this function corresponds to calculating the area under the curve from x = a to x = b.

Alternatively, we can consider the values f(a) and f(b) and visualize this scenario differently, designating various areas:

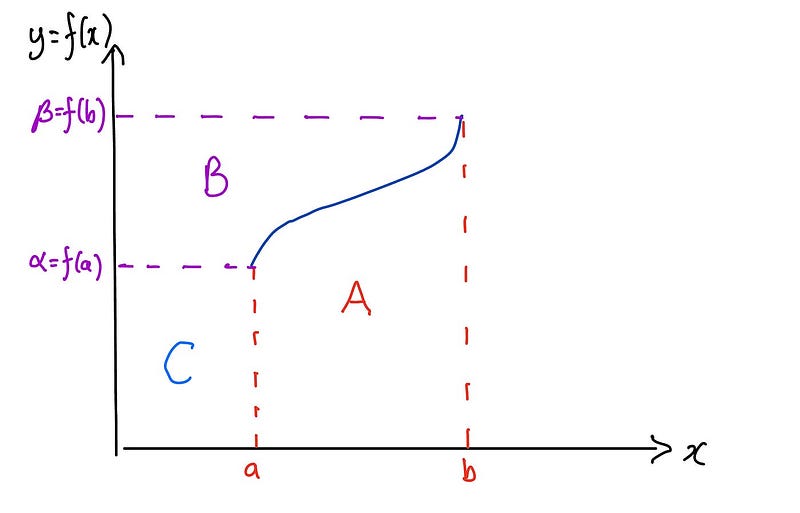
In this context, Area A represents our integral's value. We can also compute this area by finding the area of a large rectangle and subtracting Areas B and C. This process is fundamentally what integration by parts accomplishes. Let’s explore this concept further.

We can express our integral (Area A) as follows:

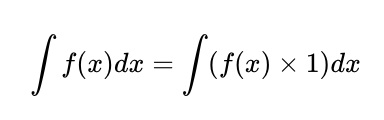
By assigning v = f(x) and du/dx = 1, we apply the integration by parts formula to yield:

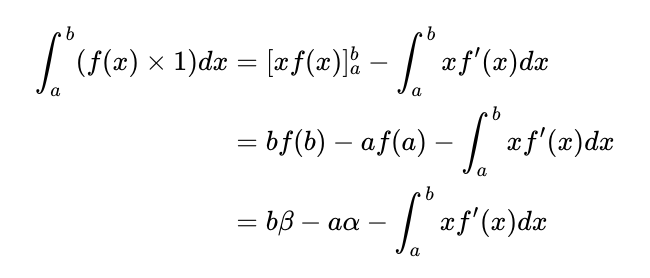
Here, b*f(b) represents the area of the large rectangle, while a*f(a) corresponds to Area C. We can also express f’(x) as dy/dx, leading us to:

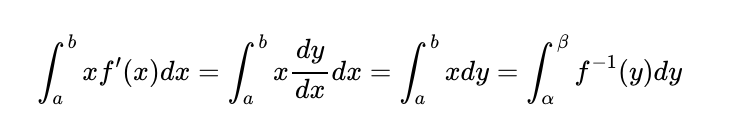
This formulation clearly illustrates that the integral equates to Area B in our diagram. Therefore, we interpret integration by parts as a geometric technique for calculating the area under a curve by subtracting various segments of a rectangle to isolate the area of interest.

Chapter 2: Expanding to Higher Dimensions

Exploring this logic in higher dimensions is equally fascinating. Consider the following integral:

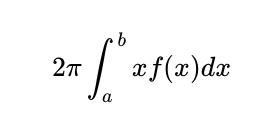
This integral signifies the volume of a "donut" formed by rotating the area beneath our curve f(x) around the y-axis. Using the integration by parts method again, with v = f(x) and du/dx = x, we can derive:

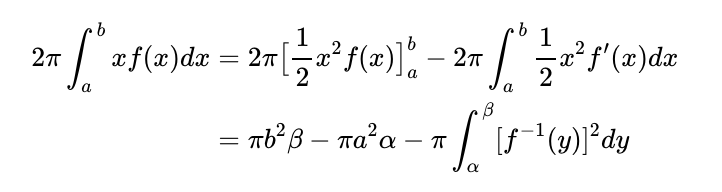
Here, the first term indicates the volume of the cylinder resulting from rotating our large rectangle around the y-axis. The second term denotes the volume of the cylinder derived from rotating Area C, while the final integral term represents the volume associated with Area B. Thus, we can view integration by parts as an indirect method for calculating the volume of a rotational shape by subtracting specific cylinder segments.

What are your thoughts on this geometric interpretation of integration by parts? I invite you to share your insights!

This video titled "Integration by Parts Intuition" delves into the foundational concepts of the integration by parts technique, providing visual aids and intuitive explanations.

In "Integration by Parts (Visualised)," viewers will see a thorough breakdown of the integration by parts method with graphical representations, reinforcing the geometric understanding of the technique.