Chapter 1: Introduction to the Determinant Problem

In this article, we delve into a particular determinant challenge inspired by the Jozsef Wildt International Math Competition. This problem, while grounded in concepts typically found at the high school or early undergraduate level, specifically requires some familiarity with linear algebra. Many problems from this competition are notoriously difficult, so it's completely understandable if you find yourself stumped!

To begin, let’s clarify what the problem requires: we need to determine the area enclosed by a specific function, the y-axis, and the vertical lines at x=1 and x=e. The nature of this inquiry strongly suggests that integration is the appropriate method to employ. However, the real challenge lies in integrating the formidable determinant.

The good news is that the determinant is presented in a manageable format, which should be kept in mind for future reference, as it frequently surfaces in mathematical discussions. This particular form is known as a Vandermonde determinant.

The primary concept is illustrated here:

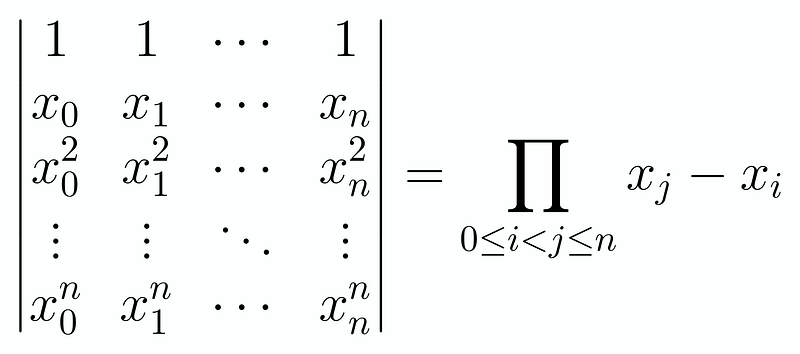
We will multiply the differences of the variables x? provided that the first index is greater than the second. For our specific case, we define x? as log x, 2log x, 3log x, and 4log x. For brevity, let’s denote L as log x, leading us to the product:

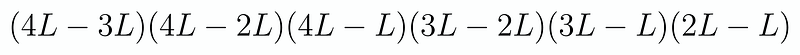
Calculating this product yields 12L². Thus, we have established our function, and the next step is to evaluate the integral.

The integral we need to consider is as follows:

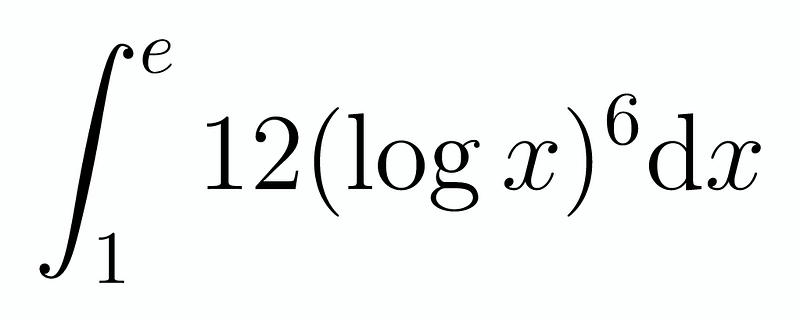
In scenarios like this, particularly influenced by the limits, it is often beneficial to perform a substitution. We can let x = e^u (or alternatively u = log x for a different approach). This substitution simplifies our integral:

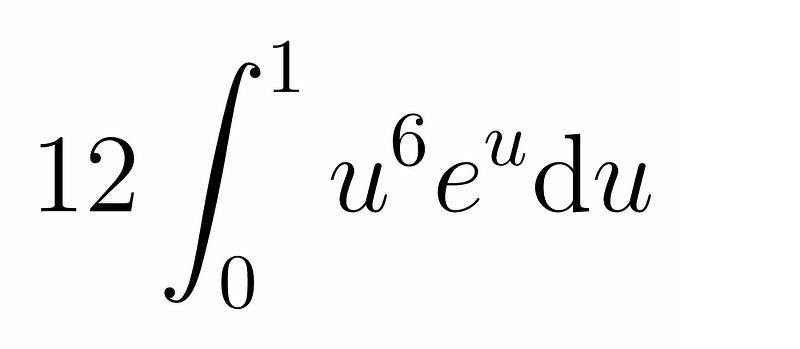
Unfortunately, while this substitution simplifies the problem, it doesn’t necessarily expedite the evaluation process. One effective strategy is to utilize reduction formulas, which we will derive next.

Consider the following equation:

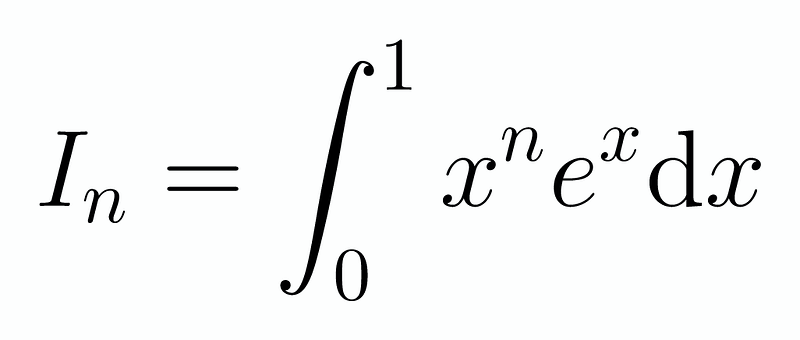
By integrating by parts, we can establish the following relationship:

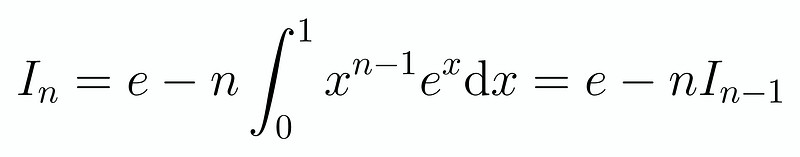
Next, we will work our way down from n = 6. Although this process may be somewhat tedious, it is significantly easier than evaluating each exponent individually. After applying this method down to I₆, which is straightforward to compute, we find that I₆ = 265e — 720. Therefore, our final result is 12 times this value.

Consequently, our ultimate answer is 12(265e — 720).

Did you find this article engaging? If so, consider supporting us!

Chapter 2: Video Explanation of the Determinant

To further enhance your understanding, check out this insightful video: