Math Problems That Seem Tough But Are Surprisingly Simple
Written on
Chapter 1: Introduction to Surds
At first glance, some math problems appear quite challenging, but they can be resolved easily with the right approach. One of the most rewarding types of math challenges is those that seem complicated initially yet become manageable once you understand the technique needed to tackle them.
Here's an intriguing problem for you to ponder. Take a moment to think about how you might solve it before I share my solution approach:
The Problem:
Simplify the following expression:
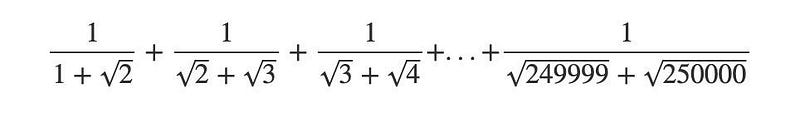
Section 1.1: Understanding Surds
Surds are mathematical expressions that involve root symbols. Mastery of surds is a fundamental aspect of the high school math curriculum across various countries. For those pursuing careers that rely heavily on mathematical computations, the ability to manipulate surds provides a valuable shortcut, particularly in situations where precision is less critical than theoretical understanding. Working with surds helps eliminate the necessity of using calculators or software for problem-solving.
Surds can be compared to algebraic expressions, as the root symbols are treated similarly to variables during manipulation. A common technique with a simple surd like ( a + bsqrt{x} ) is to multiply it by its conjugate ( a - bsqrt{x} ). This operation effectively eliminates the square root from the expression, resulting in ( a^2 - b^2x ).
Section 1.2: Rationalizing Surds
Whenever feasible, it is advantageous to work with surds that do not contain roots in the denominators. If an expression has a denominator that is a simple surd, we can rationalize it by multiplying both the numerator and denominator by the conjugate of the denominator. For instance, if our surd is ( frac{1}{a + bsqrt{x}} ) and we rationalize it by multiplying both the top and bottom by ( a - bsqrt{x} ), we arrive at the rationalized form ( frac{a - bsqrt{x}}{a^2 - b^2x} ), which limits the root to the numerator.
Chapter 2: Solving the Problem
Let's rationalize the first term of the expression we are asked to simplify. By multiplying both the numerator and denominator by ( 1 - sqrt{2} ), we find that the numerator becomes ( 1 - sqrt{2} ) and the denominator simplifies to ( 1 - 2 = -1 ). Consequently, the rationalized first term becomes ( -1 + sqrt{2} ).
Now, let's apply the same method to the second term. We discover it to be ( -sqrt{2} + sqrt{3} ), and the third term will yield ( -sqrt{3} + sqrt{4} ), continuing all the way to the final term, which results in ( -sqrt{249999} + sqrt{250000} ). The overall expression now appears as follows:
[
-1 + sqrt{2} - sqrt{2} + sqrt{3} - sqrt{3} + sqrt{4} - sqrt{4} + ldots + sqrt{249999} - sqrt{249999} + sqrt{250000}
]
Notice that all intermediate terms cancel out, simplifying our expression to ( -1 + sqrt{250000} ).
Now, while ( sqrt{250000} ) may seem daunting at first, there's a clever reason behind the selection of this term. Recognize that ( 250000 = 25 times 10000 ), where ( sqrt{25} = 5 ) and ( sqrt{10000} = 100 ). Thus, ( sqrt{250000} = 500 ). This leads us to conclude that our final sum is ( -1 + 500 = 499 ).
Feel free to share your thoughts in the comments regarding how you approached this problem and whether you were taken aback by how straightforward the solution was, given the initial complexity of the question.

This video explores how to tackle an algebraic problem that seems more complex than it actually is, revealing the straightforward methods behind the solution.
This video dives into solving an exceptionally challenging viral math problem, showcasing techniques that simplify the process significantly.