Understanding Markov's Inequality: A Simple Approach to Probability
Written on
Introduction to Markov's Inequality
In the realms of probability and statistics, Markov’s inequality serves as a crucial tool that provides an upper limit on the probability that a non-negative function of a random variable exceeds a specific positive constant. Named after the Russian mathematician Andrey Markov (1856–1922), this inequality is instrumental in linking probabilities with expected values, offering bounds for the cumulative distribution of a stochastic variable.
Imagine you are flipping N coins sequentially. A natural question arises: “What is the expected number of HEADS?” Assuming the coin flips are independent and fair, the anticipated result would be N/2 HEADS, which seems logical thus far.
Next, consider a second inquiry: “What is the probability of observing more than 2N/3 HEADS?” While it's clear that achieving at least 2N/3 HEADS is possible, can we establish a way to bound this probability? The answer is a resounding YES, and one of the simplest methods to achieve this is through the elegant Markov’s inequality.
Markov's Inequality Explained
To apply Markov's inequality, we start with a non-negative random variable X, which in this scenario represents the count of HEADS observed in N coin flips. Let E[X] denote the expected value of this variable, and let A be any positive constant. Markov's inequality states that the probability of X being at least A is bounded above by E[X]/A. Formally, we can express this as:
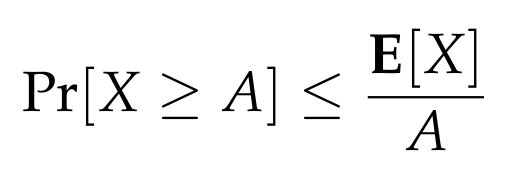
This inequality is particularly interesting when analyzing how much larger a random variable can become in comparison to its expected value. Specifically, it provides a direct upper bound for any positive t greater than 1:
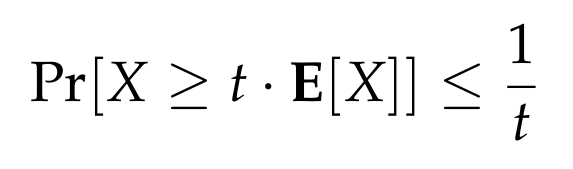
Here’s a visual description of the event that Markov’s inequality addresses:
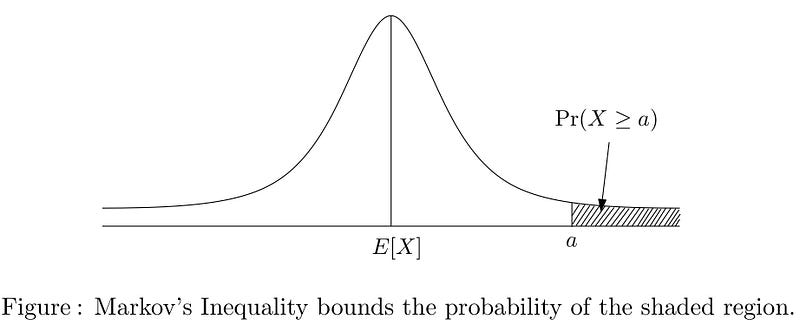
Applying Markov's Inequality: An Example
Before diving into the proof, let's apply Markov's inequality to our scenario. We aim to establish a bound on the probability of observing at least 2N/3 HEADS in N coin flips. We previously calculated that E[X] = N/2, thus leading us to:
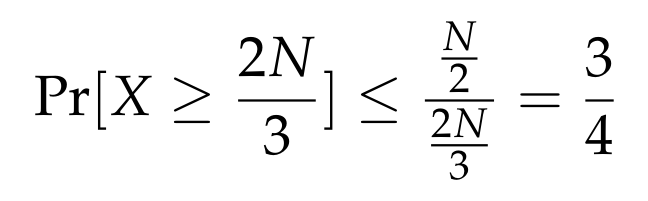
Consequently, we can conclude that with a probability of at least 1/4, we will see fewer than 2N/3 HEADS, or equivalently, more than N/3 TAILS.
Proof of Markov's Inequality
The proof of Markov’s inequality is surprisingly straightforward! We utilize the definition of expected value alongside the law of total probability, specifically the law of total expectation. We begin with:
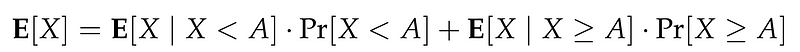
Since X is always non-negative, it follows that E[X | X < A] is non-negative as well. By focusing on the relevant terms, we can simplify our approach to:
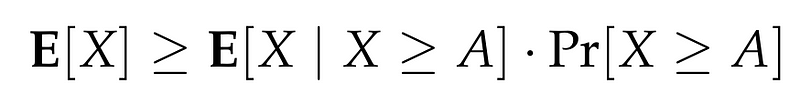
To finalize our proof, we must recognize that when conditioning X to be at least A, the expected value under this condition is at least A:
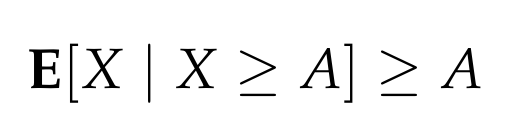
Substituting this back into our inequality gives us:
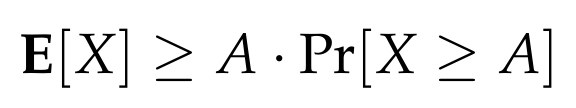
By rearranging, we arrive at:
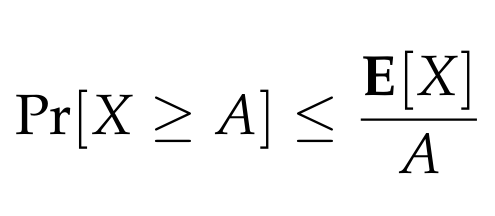
And there you have it—Markov's inequality is proven!
The Practicality of Markov's Inequality
The beauty of Markov's inequality lies in its simplicity and practicality. It frequently yields valuable bounds, even when more complex methods may not be applicable, especially when the only known information about a random variable is its expected value and the fact it remains non-negative. While there are instances where more advanced analyses may provide better results (as with the independent coin flips example, where techniques like the Chernoff bound could be applied), it is beneficial to keep this inequality in mind. And if ever needed, the proof is just a couple of minutes away!
This video, "The Beauty of Simplicity: Natural and Effortless Looks," explores the concept of simplicity, much like how Markov's inequality simplifies complex probability scenarios.