Exploring the Sum of Odd Cubes: A Challenging Math Problem
Written on
Chapter 1: Introduction to the Problem
Let’s consider an intriguing math problem from Oxford University: what is the sum of the cubes of the first ten odd numbers, specifically 1³ + 3³ + 5³ + … + 19³?
If I asked for the sum of integers from 1 to 100, you might quickly recall Gauss' formula:
S = n(n+1)/2
But what happens when we complicate it by asking for the sum of cubes like 1³ + 2³ + … + 20³? Now, if I adjust the question to focus only on the odd cubes from 1 to 19, how would you approach it?
Here’s a little hint: could you adapt the existing formula to derive a summation for even cubes?
I encourage you to pause here, grab a piece of paper, and see if you can work it out before continuing!
Section 1.1: Finding the Solution
Now, let’s dive into the solution. We know the formula for k³, so let's experiment by substituting k with 2k and observe the outcome.
The expression (2k)³ can be simplified to 8k³, allowing us to factor out the constant 8 from the summation!
We have arrived at a crucial formula. If you haven’t yet solved the problem, here’s another chance to try before moving on! Remember, the equation for odd terms can be expressed as:
Odd Terms = All Terms - Even Terms
This is a straightforward concept. If you're struggling to grasp it, writing out all the terms might clarify things!
Section 1.2: Analyzing the Summations
Let’s analyze the left-hand side of our equation more closely. It can be represented as two distinct summations.
The first summation utilizes the original formula for k³, while the second one incorporates our derived formula.
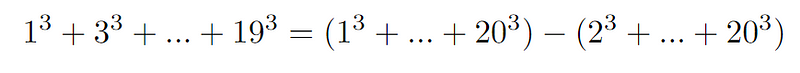
Taking a closer look, the first summation computes from 1 to 20, while the second is essentially the formula for 2k, with the factor of 2³ = 8 extracted to the front. This summation runs from 1 to 10, covering the terms 2, 4, …, 20.
Let’s substitute the values into our formula.
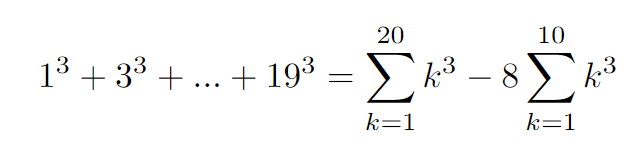
What follows is straightforward arithmetic manipulation, leading us to our final answer.
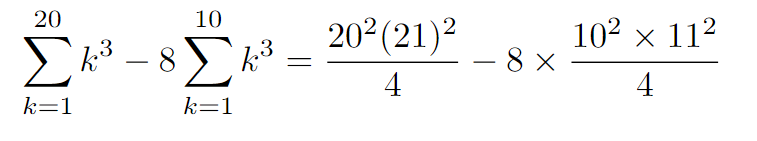
Isn’t it fascinating? Did you arrive at the same solution? I’m curious to hear your methods, so please share your thoughts!
In the first video, titled "Sum of Odd Cubes: 1³ + 3³ + ... to n terms," we further explore techniques to compute this intriguing series.
Chapter 2: Additional Insights
Now, let’s tackle another interesting series: the sum of terms like (2³-1)+(4³-3³)+(6³-5³)+... up to n terms.
In the second video, we examine how to find the sum of this series, providing additional strategies for approaching complex summations.
Thank you for joining me on this mathematical journey. I appreciate your engagement and encourage you to share this with friends who enjoy math puzzles!
