The Challenge

During my exploration, I encountered a complex double integral and wanted to verify my findings. To provide some background for those interested, I was investigating a formula related to the number of twin primes below a specified number, utilizing the prime counting function and techniques from complex analysis. Now that we have that context, let's proceed.

When faced with a troublesome problem involving a highly discontinuous function, what is one to do? Typically, you would grab your laptop, pour a large cup of coffee, and open a code editor. For me, Python is my language of choice, so I began by creating an empty Python file, expecting to complete this task in about 10 to 15 minutes.

I was mistaken! The reason? Crafting the necessary custom functions, such as identifying prime numbers and counting them with loops, was straightforward. However, the real challenge arose when I attempted to integrate them.

"Usually, Python’s scientific libraries come to the rescue, but in this case, they let me down."

SciPy has a function called quad designed for this type of task, which made me optimistic about a quick resolution. Typically, Python’s scientific libraries are user-friendly, but this time, they failed me. The issue was that my integrand for the double integral contained a pole within the integration interval.

A Simple Analogy

Suppose you aim to compute the following integral:

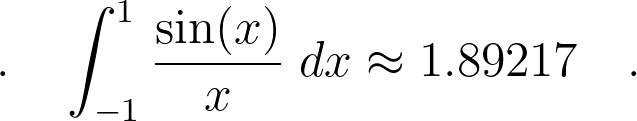
I actually tried this example and it didn’t yield the expected results. While the function behaves well around zero, my attempts to calculate it resulted in a value of nan. At that moment, the reason became clear.

SciPy employs methods akin to Riemann sums or the Trapezoidal rule for integration, which necessitates dividing the integration interval into numerous smaller segments. To compute the areas of these small rectangles, it must evaluate the function at all the endpoints of these segments—one of which was (very close to) zero!

Naturally, attempting to divide by zero in Python raises a ZeroDivisionError. According to SciPy’s documentation, there are potential workarounds, such as specifying known poles (which requires prior knowledge of the function's poles, a luxury not always available). Unfortunately, this approach did not work for my double integral, despite being effective for the simpler example above.

The Objective

The aim of this introduction is clear:

• A numerical integration tool should focus solely on convergence—not on identifying poles.
• Users shouldn't be burdened with finding poles or even thinking about them.
• The tool should be adaptable, allowing modifications to suit specific needs, such as adjusting the error versus runtime parameters (more on this shortly).
• The error messages should be meaningful and comprehensible.

Frustrated, I resolved to develop my own tool.

After this realization, I needed another cup of coffee to contemplate the design of this tool. There are countless approaches to achieve this, but I opted for a lightweight design. I believe that such a tool must be flexible enough to meet user requirements.

Let’s Build the Tool!

I chose an object-oriented design, constructing a class around the function to be integrated. This structure would enable users to easily add features in the future and retain meta-information about calculations, such as error intervals.

The Code

To begin with, this program primarily relies on NumPy. For convenience, we will also import quad:

If you haven't installed these packages, you can do so with:

pip install numpy quad

or pip3 depending on your operating system.

To ensure compatibility, make sure to run this code with Python 3.

Let's create the Integrate class:

class Integrate:

# Class implementation here

A few comments are necessary. First, I will log the error, which will become relevant shortly. Second, I've defined a sign attribute to handle cases where the bounds of the integral are reversed. This allows calculations even when the lower limit exceeds the upper limit, demonstrating how this can be handled elegantly.

Next, we will define the primary integration method:

def integrate(self, function, lower_bound, upper_bound):

# Integration logic here

I utilized the trapezoidal rule (essentially an average of left and right Riemann sums), which is expected. You might be curious about the large try/except block—this is a crucial feature. It ensures that if a division by zero occurs, it will be managed gracefully without requiring user intervention.

We also retain the calculated error for those who wish to perform interval arithmetic or verify the accuracy of the result.

Using Our Tool

Now, how do we utilize our newly created tool? Suppose we want to integrate the function from our earlier example.

result = integrate_instance.integrate(my_function, 0, 1)

This resolves the "0/0" situation when x = 0.

Now we obtain a result of approximately 1.892166, which is quite satisfactory!

However, our work isn't finished. We still need to tackle the double integral, and we currently lack a functional tool for this.

To address this, we need to generalize our code for double integrals. First, we should clarify the potential errors we might encounter. To facilitate this, we will create a custom error class in Python by inheriting from Exception:

class IntegrationError(Exception):

pass

Furthermore, since the input intervals will now be a list of lists, a potential solution could be structured as follows:

def double_integrate(self, function, intervals):

# Double integration logic here

Important Note: This is not optimized for performance; we could enhance it with vectorization in NumPy.

You can adjust the precision parameter to meet your needs. A higher value will yield more accurate results, but it will also require more computation time. This is where the error attribute becomes useful. Consider trying to optimize this code as an exercise!

While we could extend this to triple integrals, let's focus on single and double integrals for now.

Let’s See It in Action!

Allow me to demonstrate how our tool functions. Imagine you’re working on a project in Python and suddenly need to approximate the following integral:

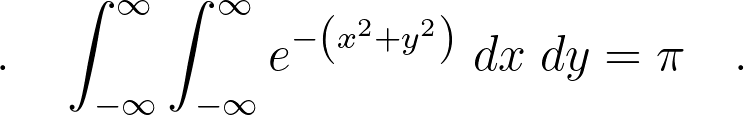
Now, equipped with the right tool, you can tackle this problem. At the beginning of your file, import your new integration engine:

from my_integration_tool import Integrate

Later in your project, you can solve the integral:

result = integrate_instance.integrate(my_function, a, b)

This will yield an output of:

The result is 3.1415926535897944

The accuracy of this result is -1.7319479184152442e-14

This is impressively close! In fact, the true value of pi starts with 3.141592653589793238… and our error range confirms we captured the first 14 digits accurately (at least within our limits of integration—bear in mind, we might be missing the "tails" of the function). By increasing the precision parameter or adjusting the integral limits, we could achieve even more accurate results.

The takeaway here is significant: although the double integral should encompass the entire real plane, we can ensure that within our specified interval, we can get arbitrarily close to the true value—and we can verify this through our error attribute. It’s a balance between accuracy and runtime.

Now I can return to my research, and if you face similar challenges or wish to deepen your Python knowledge, feel free to use or enhance this code.

You can clone the complete repository here.

After seven cups of coffee, I can finally sleep soundly. I just hope I won’t be haunted by frantic Riemann sums in my dreams.

Oh, and what about integrating with polar coordinates? Perhaps that will be our next adventure.