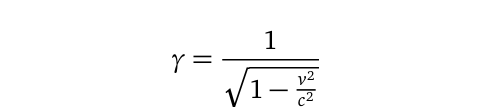
Problem Definition

The existence of the Lorentz factor introduces significant challenges in calculating relativistic mass, energy, momentum, and time dilation, particularly as velocities approach the speed of light in a vacuum. As the square speed ratio ( v^2/c^2 ) nears unity (1), mathematical singularities become unavoidable. This issue is exacerbated for objects moving at comparatively low speeds. Consequently, physicists often resort to a binomial approximation of the following form:

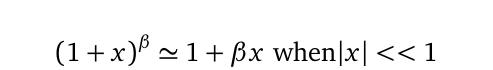
From the equation above, it becomes evident that computations at the constant speed of light (( c )) yield infinite values, complicating relativistic and quantum mechanical operations related to the Lorentz factor. This challenge was notably highlighted by Paul Dirac when he laid the groundwork for relativistic quantum mechanics. The most pertinent equations regarding relativistic mass-energy-momentum, which form the basis of special relativity as articulated by Einstein, can be expressed as:

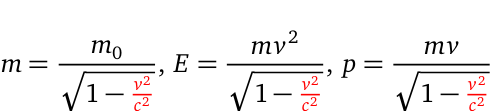
The pressing question remains: what occurs when ( v = c ) in the above equation? To understand this, we can first examine the scenario when ( v = 0 ). In this case, the object is stationary, and thus its relativistic mass equals its rest mass, with both kinetic energy and momentum equating to zero. As the object accelerates, these three quantities become distributed across space and time, transitioning from rest to classical limits before quantum effects emerge. In the forthcoming sections, we will investigate a finite solution for this system.

Seeking a Finite Solution

Rather than relying on binomial approximation, we can introduce a renormalization parameter, denoted as ( j ). Renormalization serves as a method in quantum field theories to manage infinities arising from calculated values that would otherwise be nonsensical. We can express the square speed ratio as a function of this ( j ):

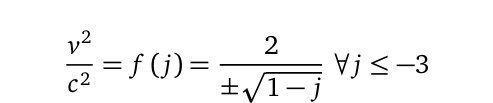
For now, it suffices to note that a ( j ) value of -3 results in ( v^2/c^2 = 1 ), representing the maximum limit. The theorem described by this equation holds true for all values within that range, as long as we acknowledge the theoretical limit of ( c ), the speed of light in a vacuum. Testing can be conducted at various values such as -8, -15, -24, -35, and so on.

Physical Implications of Renormalization

Assuming the mathematical framework of the equation is valid, what are the physical implications of the renormalization parameter ( j )? Its value appears to be regime-specific, implying it varies based on the particle's location and speed. For example, we can define ( j ) for electrons within a hydrogen atom as follows:

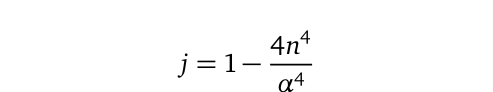
Where ( n ) represents the electron shell number, also known as the principal quantum number. The constant ( alpha approx 1/137.06 ) is known as the fine structure constant, a dimensionless value that frequently appears in discussions of elementary particles. This hypothesis can be validated by setting ( n = 1 ) for the ground-state electron in a hydrogen atom, yielding a corresponding ( j ) value and an exact speed of the electron at approximately ( v = 2187308.1716 , m/s ).

Furthermore, the renormalization parameter can be expressed as a function of speed, applicable to any non-stationary object:

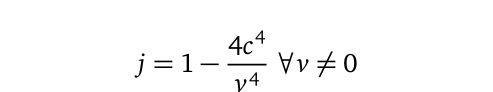
To verify the accuracy of this equation, one can substitute known speed values ( v ) to estimate ( j ), which may then be employed to calculate the energy levels of electrons in hydrogen. From our earlier example, when ( v = c ), ( j ) must consequently reduce to a maximum of -3.

Comparison with the Dirac Equation

To effectively implement the derived renormalization, it is essential to note that the denominator of the previous equation can take both negative and positive values. In all cases, we choose the negative, ensuring the speed is consistently returned by the following function:

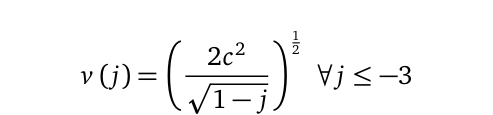
Substituting this expression back into any of the mass-energy-momentum equations results in the elimination of singularities. For instance, applying this to the energy equation yields:

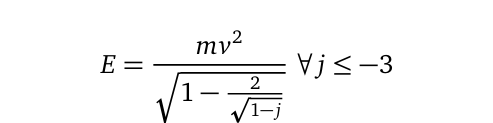
The theoretical implication is that at the speed of light in a vacuum, the energy of a particle should conform to the following expression:

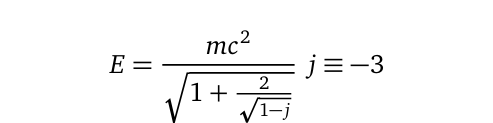
Meanwhile, Dirac’s precise energy equation predicts the relativistic quantum mechanical characteristics of hydrogen atoms as follows:

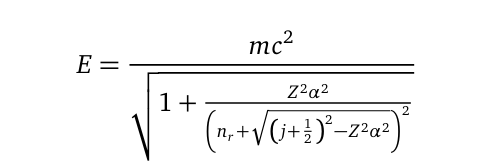
Here, ( Z^2alpha^2 ) is a small, non-integer value, while the principal quantum numbers in Dirac's equation are expressed through the linear relation ( n = n_0 + k ), where ( n_0 ) is the quantum number at a specific radius ( r ), and ( k ) is a non-zero integer defined by the relation:

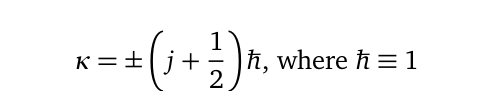
Note that the notation ( j ) in the energy equations differs from that in the previous sections, as it is specific to Dirac's formulation.

A notable similarity exists between the equations concerning energy derived here and those from Dirac’s work, particularly in the second term under the square root in the denominator of the right-hand side.