Section 1.1: The Fundamentals of Huffman Coding

Developed by David A. Huffman in 1952, Huffman coding is a variable-length prefix coding technique. It works by assigning shorter binary codes to symbols that are used often, while less common symbols receive longer codes. This creates an efficient compression system where no code serves as a prefix for another, thus ensuring clear decoding without confusion.

Section 1.2: Step 1 - Frequency Analysis

Before we can encode, we must analyze the frequency of each symbol in our input string. Let’s take a look at the string "AADCABCA" to create a frequency table:

• A: 4 occurrences
• B: 1 occurrence
• C: 2 occurrences
• D: 1 occurrence

Section 1.3: Step 2 - Building the Huffman Tree

Next, we will construct a Huffman tree based on the frequencies we just calculated. We begin by creating nodes for the least frequent symbols, which are B and D in this case. Starting with individual nodes for each symbol, we repeatedly combine the nodes with the lowest frequencies until only one node remains, forming the root of the Huffman tree.

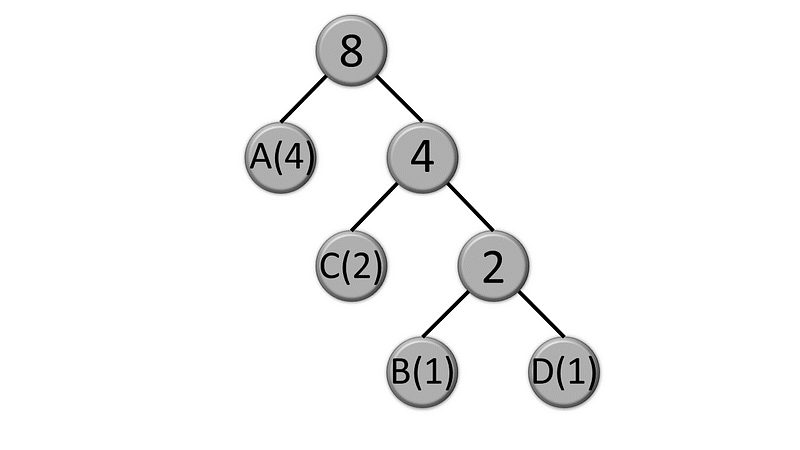
At this point, you have constructed your Huffman tree (or a dictionary).

Section 1.4: Step 3 - Assigning Binary Codes

With the Huffman tree established, we now proceed to assign binary codes to each symbol. To do this, we traverse the tree from the root to each leaf, adding '0' for a left branch and '1' for a right branch.

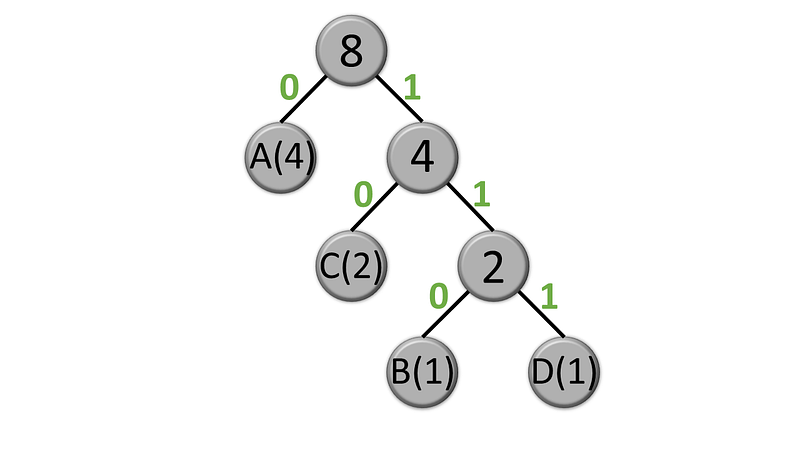
The resulting binary codes are as follows:

• A: 0
• B: 110
• C: 10
• D: 111

Section 1.5: Encoding the String “AADCABCA”

Now that we have the Huffman codes for each symbol, we can encode our input string “AADCABCA” using these codes:

• A: 0
• A: 0
• D: 111
• C: 10
• A: 0
• B: 110
• C: 10
• A: 0

Combining these codes results in the Huffman-encoded representation of “AADCABCA”: 00111100110100.

To put this into perspective, if both the compressor and decompressor have the dictionary, the original string consists of ASCII characters totaling 64 bits (8 characters x 8 bits each), while the Huffman-encoded output is only 14 bits long, leading to a significant reduction of 50 bits!