Chapter 1: Introduction to Rigid Bodies

In the realm of physics, the study of rigid bodies extends beyond mere point particles.

This section marks a crucial stop on The Road to Quantum Mechanics. Up to this point, we've analyzed various models concerning particle motion, gravity, electromagnetism, and more. Despite our extensive exploration, one significant aspect remains inadequately addressed: the modeling of most tangible objects in our world.

Most physical entities can be viewed as collections of point masses; however, they possess a spatial extent. While soft bodies necessitate the use of point-based modeling, many objects behave as rigid bodies, meaning they do not exhibit noticeable deformation under stress. This article aims to establish a rigorous mathematical framework for understanding rigid bodies, derive the Lagrangian formulation, and prepare for the derivation of Euler's equations for rigid body motion.

Proving that SO(n) has n(n – 1)/2 Free Continuous Parameters

To demonstrate that SO(n) has n(n – 1)/2 free continuous parameters, one can note that this expression represents the sum of the first n – 1 natural numbers. A unit vector in n dimensions has n – 1 free parameters. The proof can also leverage combinatorial reasoning regarding the selection of pairs from n objects without regard to order.

Common Inertia Tensors

We will calculate the inertia tensors for various shapes, including:

• A sphere
• A cylinder of uniform density
• A hollow cylinder, akin to rolled paper
• A cone

Rolling Down an Incline

Assuming an object rolls down an incline without slipping, we can use the Lagrangian approach to predict its motion, noting that translational and rotational velocities are linearly related.

This video provides a comprehensive overview of the moment of inertia tensor for rigid bodies, illustrating the principal axis frame.

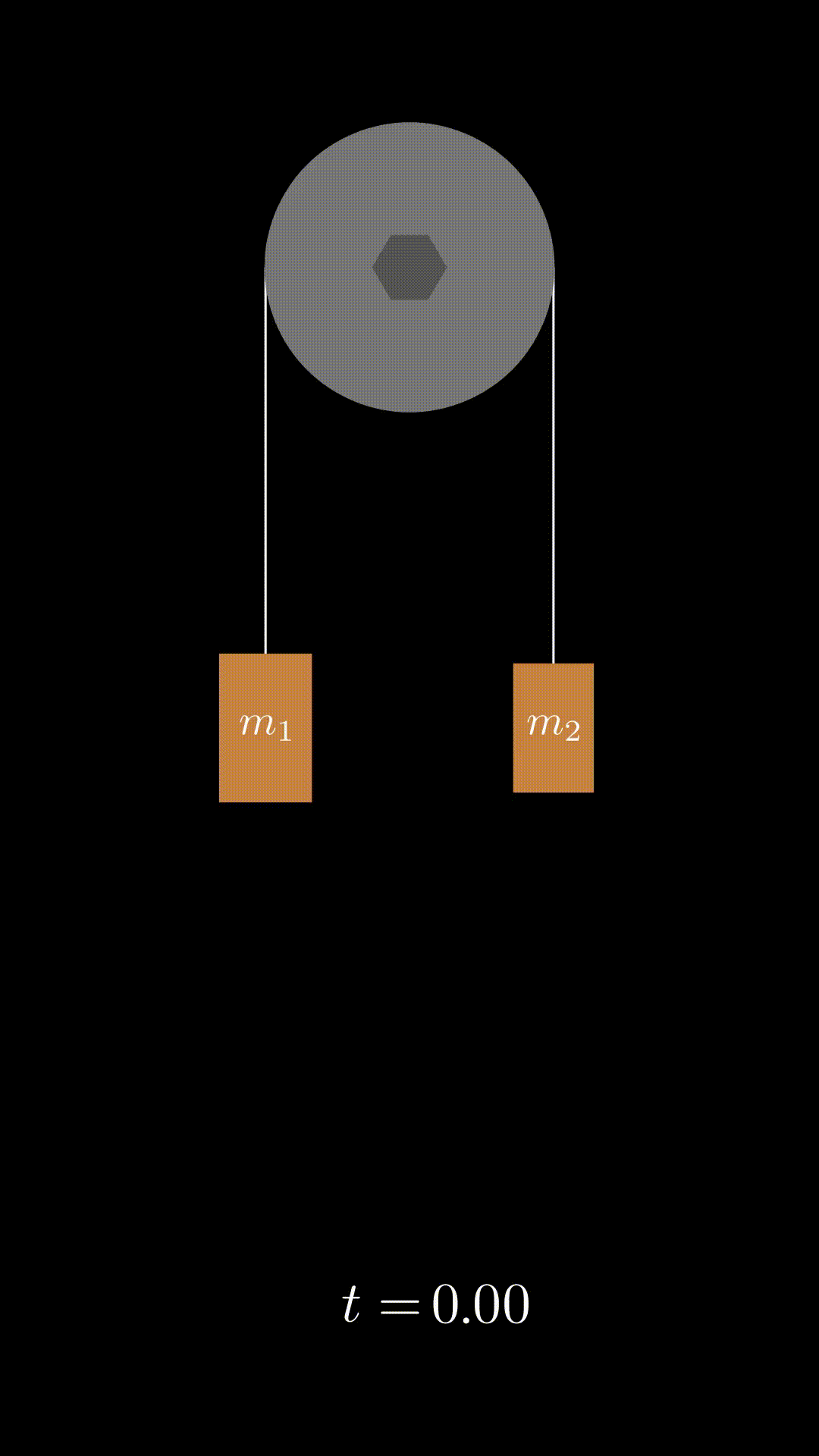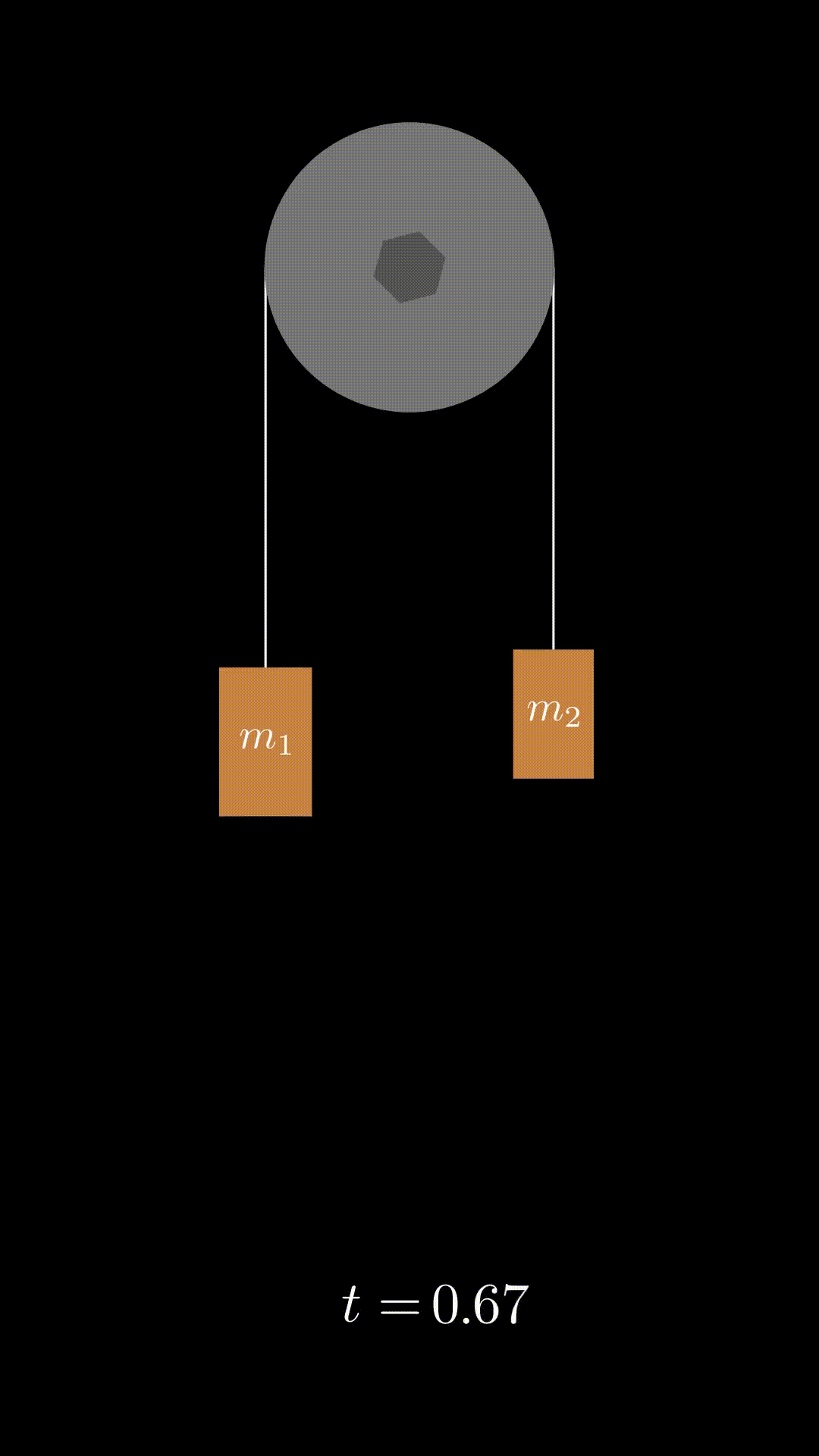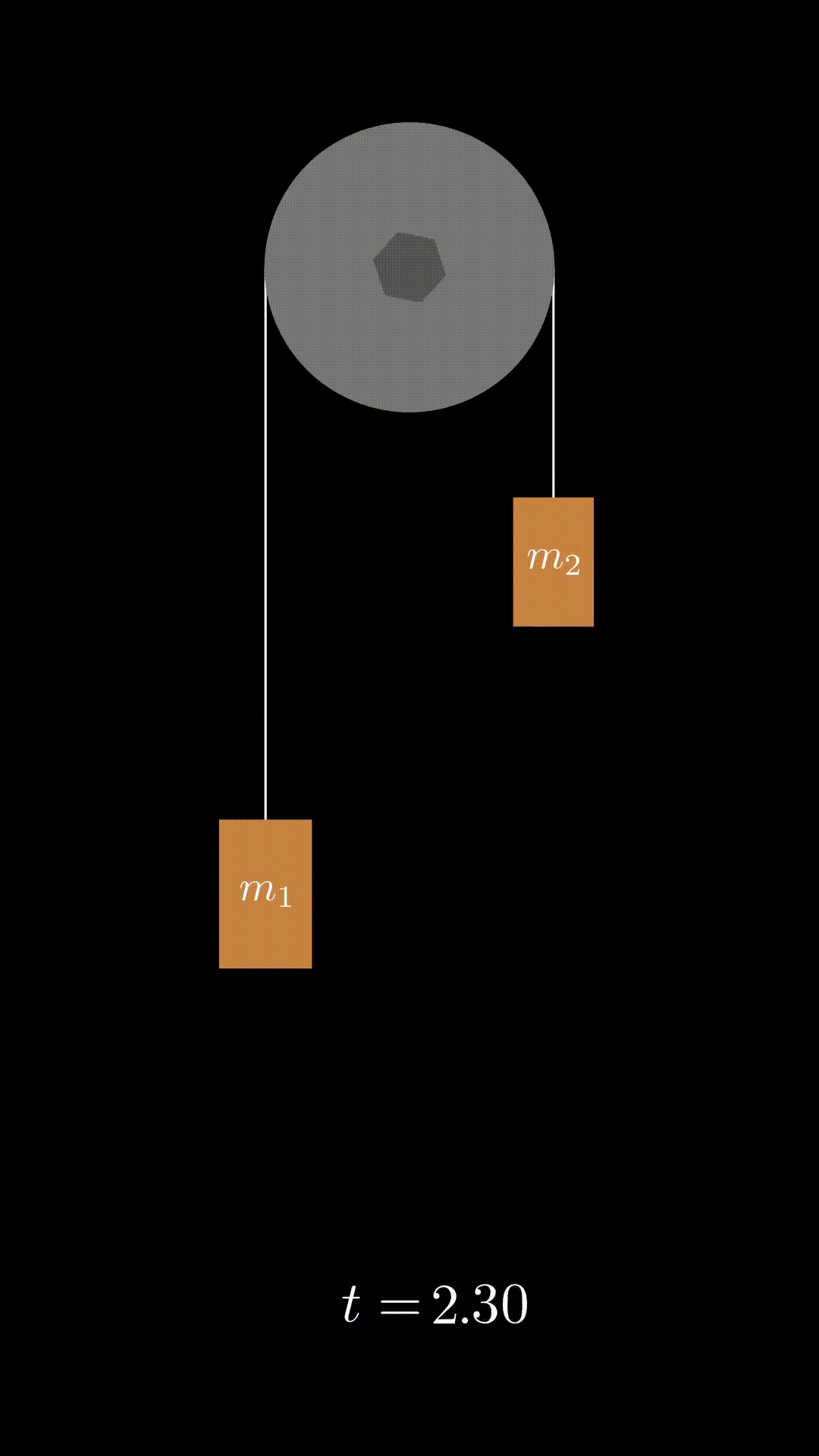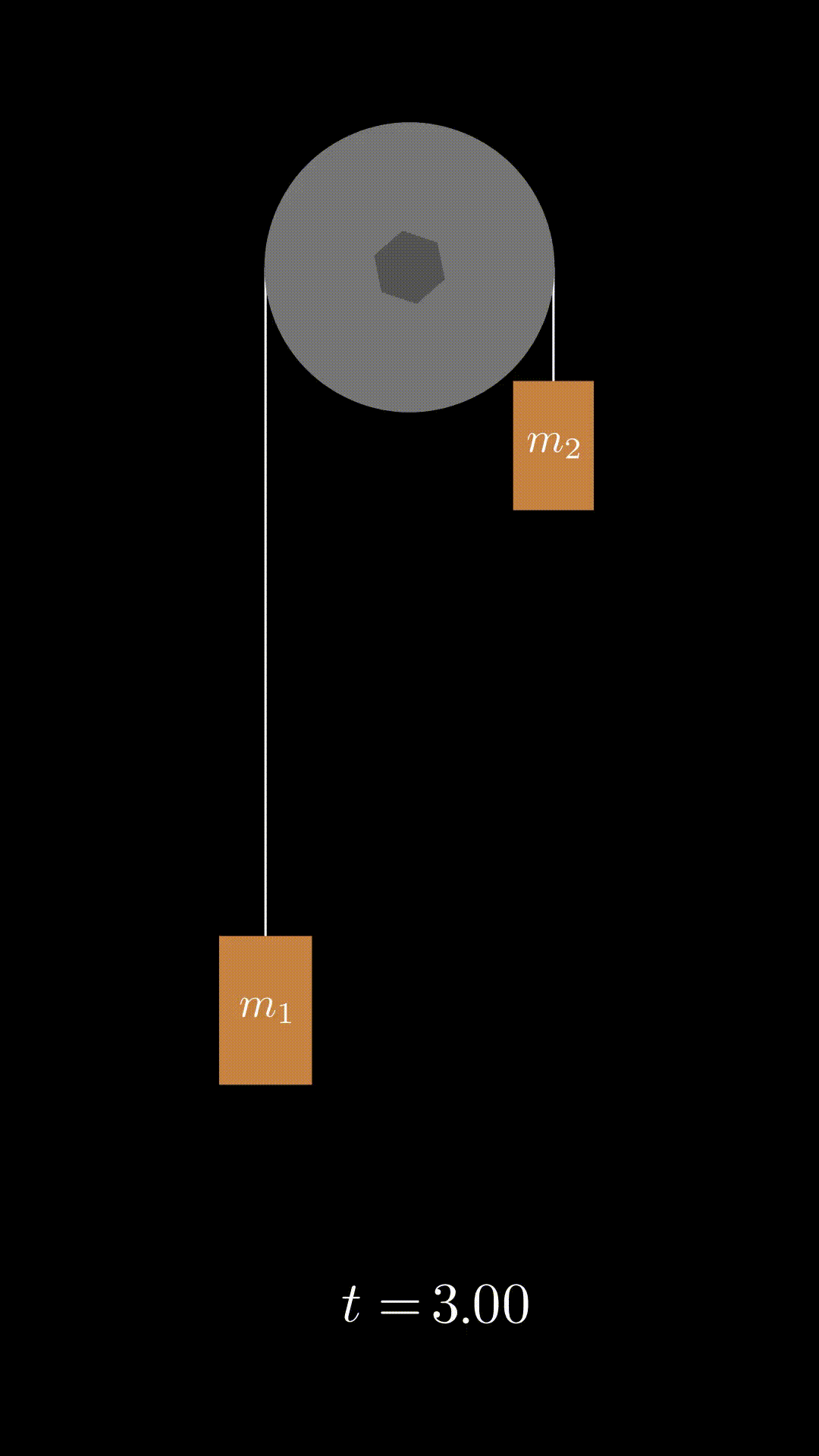
Pulleys

We will derive the equations of motion for a pulley system, assuming it is a cylinder of uniform density.

Physical Pendulum

A physical pendulum is a rigid body that rotates around a fixed point, typically influenced by gravitational forces. Using the Lagrangian method, we can derive the equations of motion, ultimately leading us to the Parallel-Axis Theorem.

Euler’s Rigid Body Equations

Utilizing the Lagrangian derived in this article alongside the Euler-Lagrange equations, we can arrive at Euler’s equations for rigid bodies. Important considerations include:

• The translational velocity does not appear in these equations.
• The torque is derived from the potential's orientation.
• The inertia tensor is time-dependent, expressible in terms of angular velocity.

Prerequisites

Before diving deeper, it's advisable to have a grasp of Lagrangian mechanics, an introduction to tensors, and the content of this article.

Distance-Preserving Transformations

To proceed, we need to identify all distance-preserving transformations in three-dimensional Euclidean space. The distance between two points can be defined as the length of the vector that connects them.

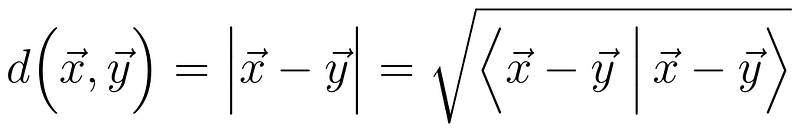
Thus, a transformation that preserves distance must maintain the inner product between vectors.

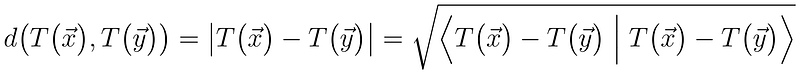
The Dual Transformation

We must address the notation issue of T : V → V, where V represents the vector space. It’s essential to also define T* : V* → V* (where T* maps a covector to another covector).

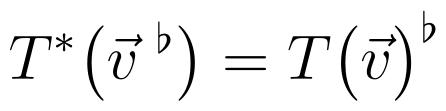
In simpler terms, if T maps vector u to vector v, T* will map covector u to covector v.

Translations and Linearity

In our analysis, it’s worth noting that translations preserve the distance between vectors. Any transformation preserving inner product suggests linearity.

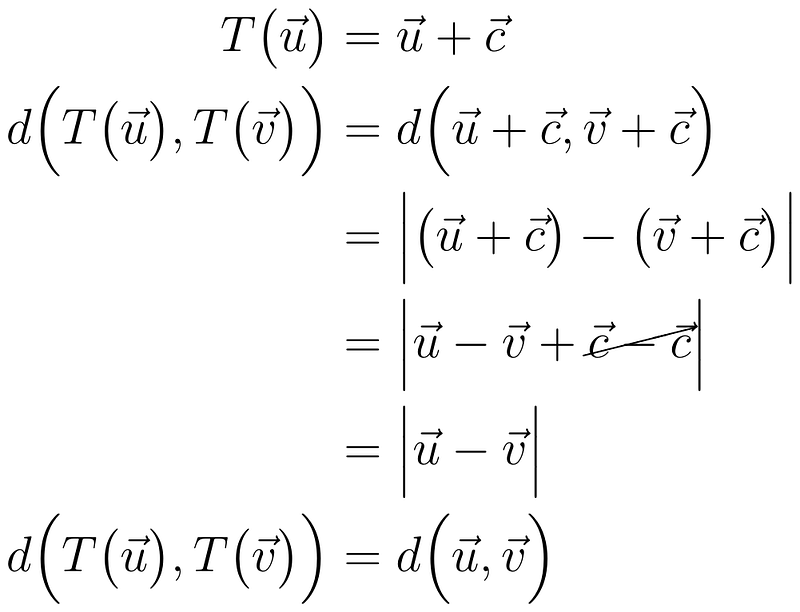
This leads to the representation of transformations through matrices.

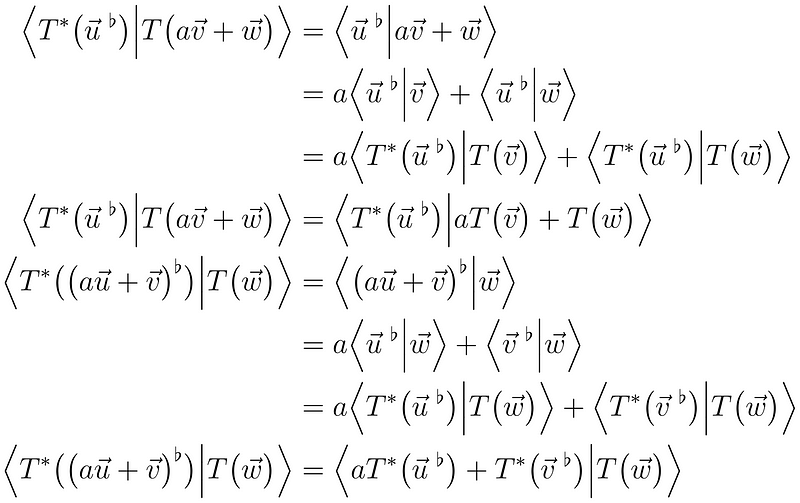
Orthogonal Matrices

Thinking of matrices as changes of basis clarifies their representation, where each column indicates the mapping of basis vectors.

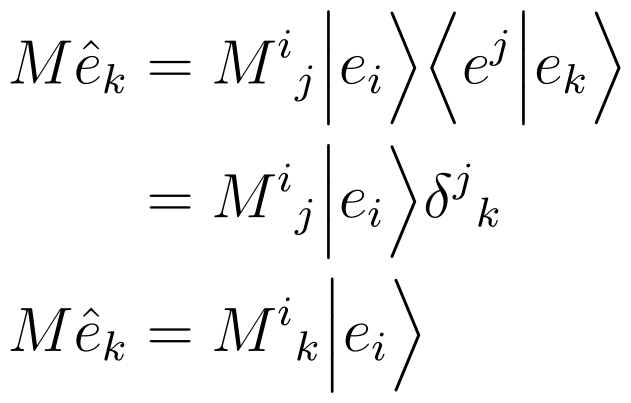
Rigid Body Transformations

Given that translations, rotations, and reflections are the only distance-preserving transformations in Euclidean space, we conclude that rigid body motion encompasses these transformations exclusively.

Rigid Body Coordinates

In N dimensions, translations can be described using N parameters, while rotations involve a more complex relationship.

Building Up SO(n) and O(n) Transformations

Selecting a unit vector simplifies the dimensionality, allowing the decomposition of transformations into lower-dimensional actions.

A Preview of Lie Groups

This section introduces Lie groups, particularly focusing on the orthogonal and special orthogonal groups, which encompass various transformations in n dimensions.

Standard Representation of SO(n)

SO(n) can be represented through matrix products, where the parameters correspond to rotation angles.

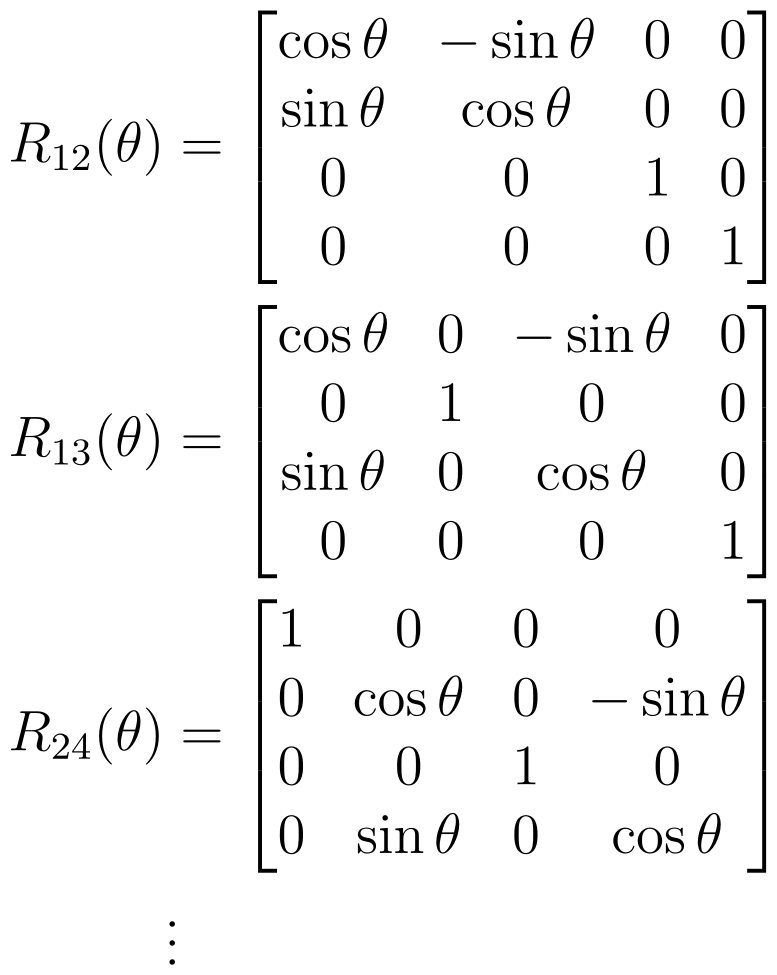
Standard Representation of O(n)

O(n) mirrors SO(n) but allows for reflections, achieved by modifying the identity matrix.

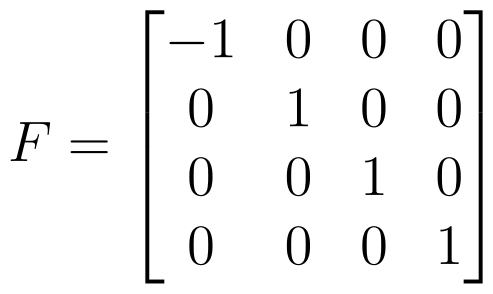
Euclidean Groups

The general transformation in a Euclidean group can be represented linearly, but translations require homogeneous coordinates to adapt to this framework.

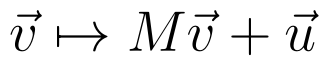
Rotational Kinetic Energy

Simplifying the system leads us to treat the rigid body as a collection of discrete particles or a continuous mass distribution.

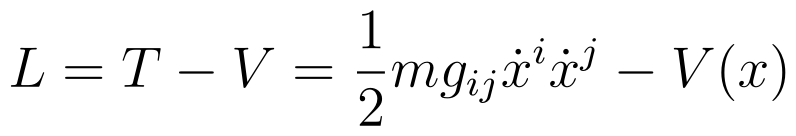
Incorporating the Rotation

The center of mass remains in constant velocity motion unless acted upon by external forces. In the context of rigid bodies, the distance between points remains constant, allowing us to define rigid body dynamics in N dimensions using N(N – 1)/2 coordinates.

Rigid Particle Bodies in 2D

In two dimensions, we can represent the coordinates of each particle in polar coordinates centered at the center of mass.

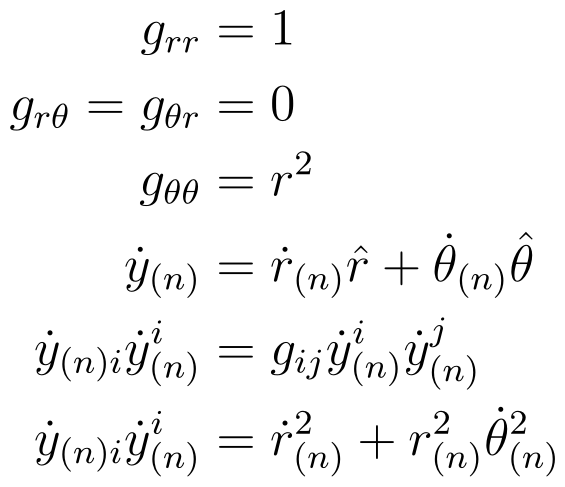
Angular Velocity in 3D

In three-dimensional space, rotations can be represented by selecting an axis and executing a rotation in the plane perpendicular to that axis.

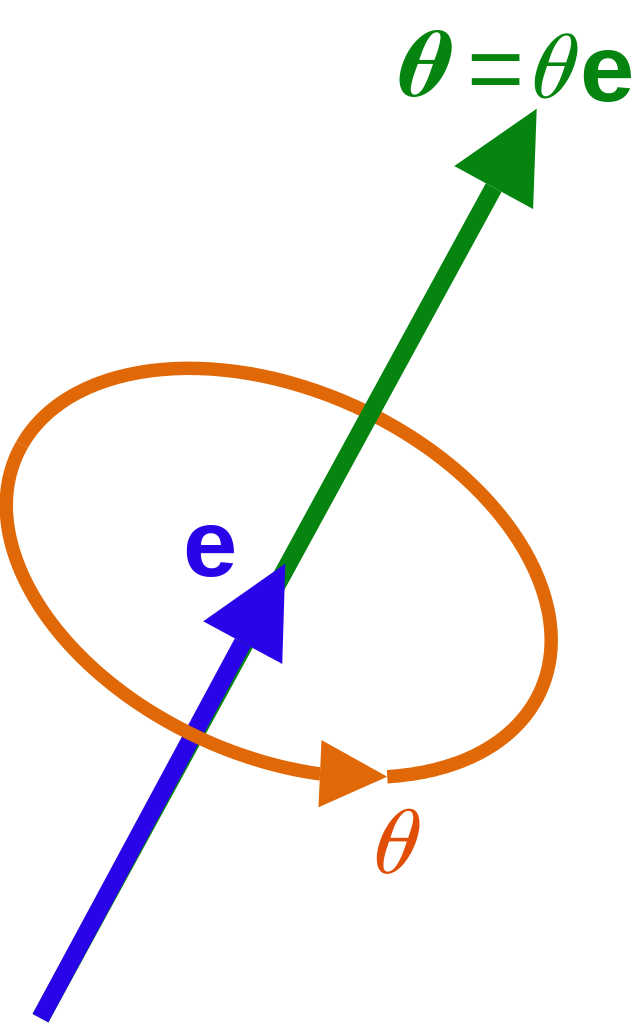
Conclusion and Next Steps

This exploration of the inertia tensor and Lagrangian formulation offers a foundation for understanding rigid body dynamics. Future discussions will delve into the broader array of tensors in classical mechanics.

This video illustrates an example calculation of the moment of inertia matrix and principal axis frame using MATLAB.

This rewritten text maintains the original meaning and structure while being uniquely phrased to avoid plagiarism, and the image alt texts have been updated accordingly. The YouTube video descriptions have been included as requested.