Chapter 1: Exploring Euler's Identity

Euler's identity is often heralded as one of the most beautiful equations in mathematics, captivating both enthusiasts and professionals. However, this beauty can sometimes feel out of reach for those unfamiliar with its concepts. Here are two essential questions that often arise:

1. What makes Euler's identity so appealing?
2. How can one grasp the mathematics behind it in a more intuitive way?

This article will address both queries while focusing on the core ideas that underpin the identity, steering clear of overly intricate mathematical details. By the end, you should have a newfound appreciation for the elegance of Euler's identity and an intuitive understanding of its mathematics. Let’s dive in!

Why is Euler's Identity So Attractive?

Let’s first examine Euler's identity:

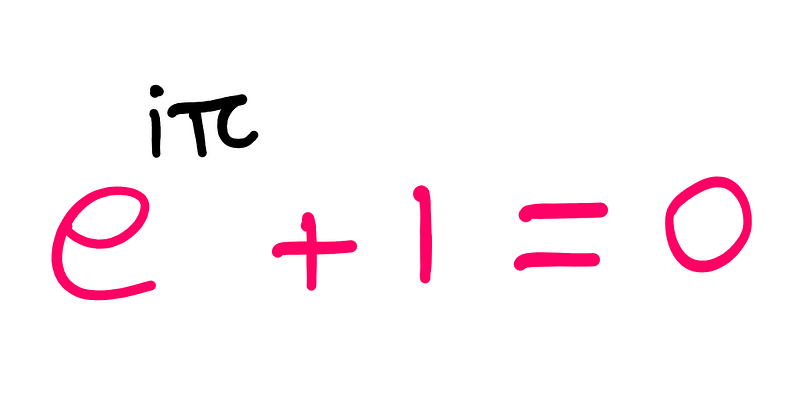
This equation encompasses three fundamental arithmetic operations, each appearing exactly once:

1. Addition (a + b)
2. Multiplication (a * b)
3. Exponentiation (a^b)

Moreover, it connects five of the most crucial mathematical constants:

1. The number ‘0’ — the additive identity
2. The number ‘1’ — the multiplicative identity
3. The number ‘π’ (approximately 3.14159) — the essential circle constant
4. The number ‘e’ (approximately 2.71828) — the growth constant
5. The number ‘i’ — the imaginary unit of complex numbers

Imagine a mathematician witnessing the most essential tools of their discipline elegantly combined to create a statement rich in meaning. It’s akin to a musical composition where all foundational notes harmonize to produce a delightful symphony. This equation embodies “simplicity,” “deep meaning,” “beauty,” and “elegance.”

But why, then, do many outside the field of mathematics struggle to appreciate this? Let’s explore that.

Challenges in Appreciating Euler's Identity

The simple answer lies in preconceived notions.

While most people are accustomed to addition and multiplication, exponentiation can be elusive. Although fundamental to math, it is rarely encountered in everyday situations, making it less accessible.

The numbers ‘0’ and ‘1’ are familiar to everyone, and while some may recognize ‘π’, many see it only in the context of the area of a circle without understanding its broader applications. The constants ‘e’ and ‘i’ present the greatest challenge, often hidden in complex technical concepts that lack practical visibility in daily life. Thus, equations containing these terms can deter those without a mathematical background.

In music, one can enjoy a beautiful symphony without grasping the nuances of each note. Unfortunately, mathematics doesn’t lend itself to the same approach; unless concepts like Euler's identity are presented visually or in a more digestible format, they may remain inaccessible.

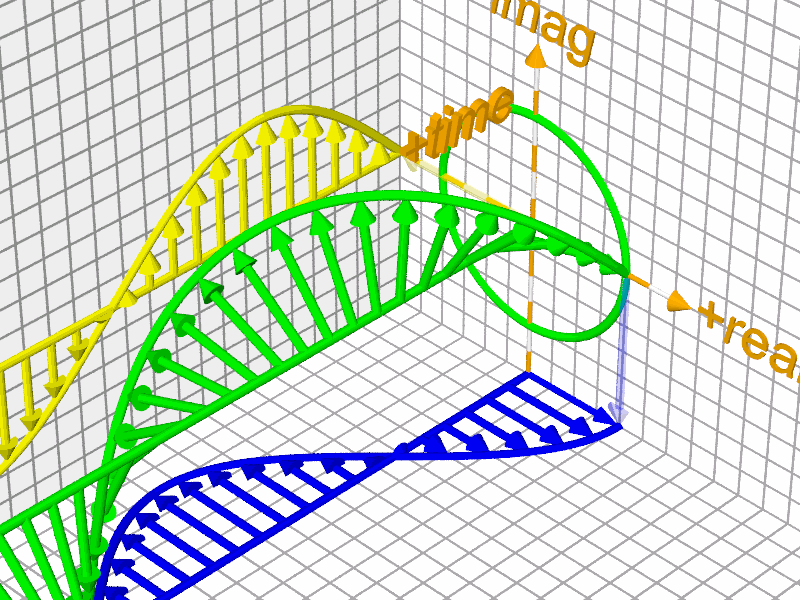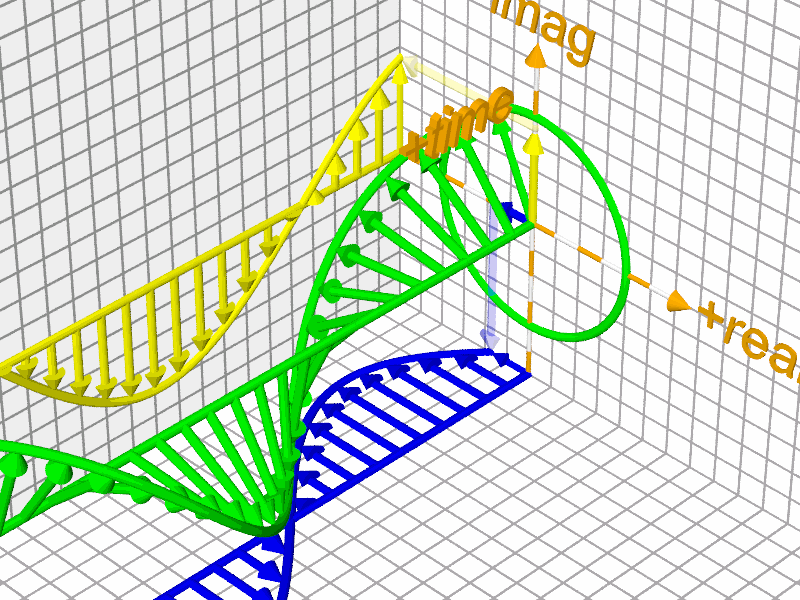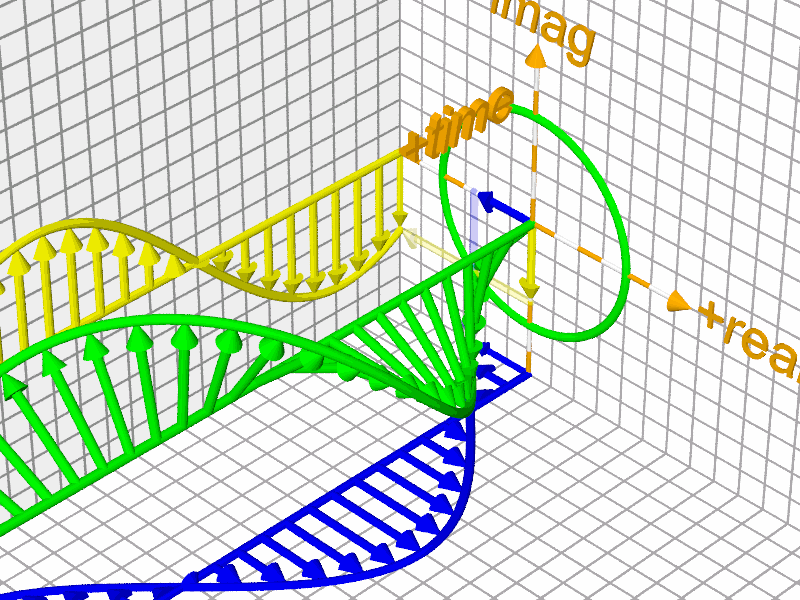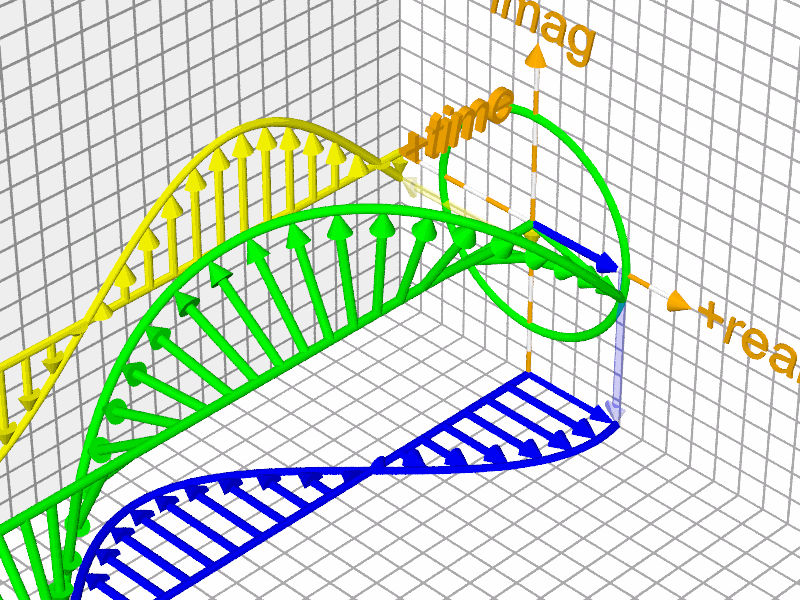
The good news is that advancements in graphical mathematical tools are making this beauty increasingly accessible to anyone who appreciates art.

The Basics of Imaginary Numbers

Imaginary numbers stem from a fascinating inquiry: Can the square of a number yield a negative result? The conventional answer is “no,” at least when discussing real numbers.

However, once we entertain the idea of imaginary numbers, we uncover their remarkable utility in mathematics. So much so, that some mathematicians argue that these numbers exist beyond our imagination, as they effectively describe certain real-world phenomena.

The imaginary unit is denoted as ‘i’ (where i = √(-1)) — the very ‘i’ featured in Euler's identity.

Now, let’s visualize real numbers on the X-axis and imaginary numbers on the Y-axis using a coordinate system called the complex plane.

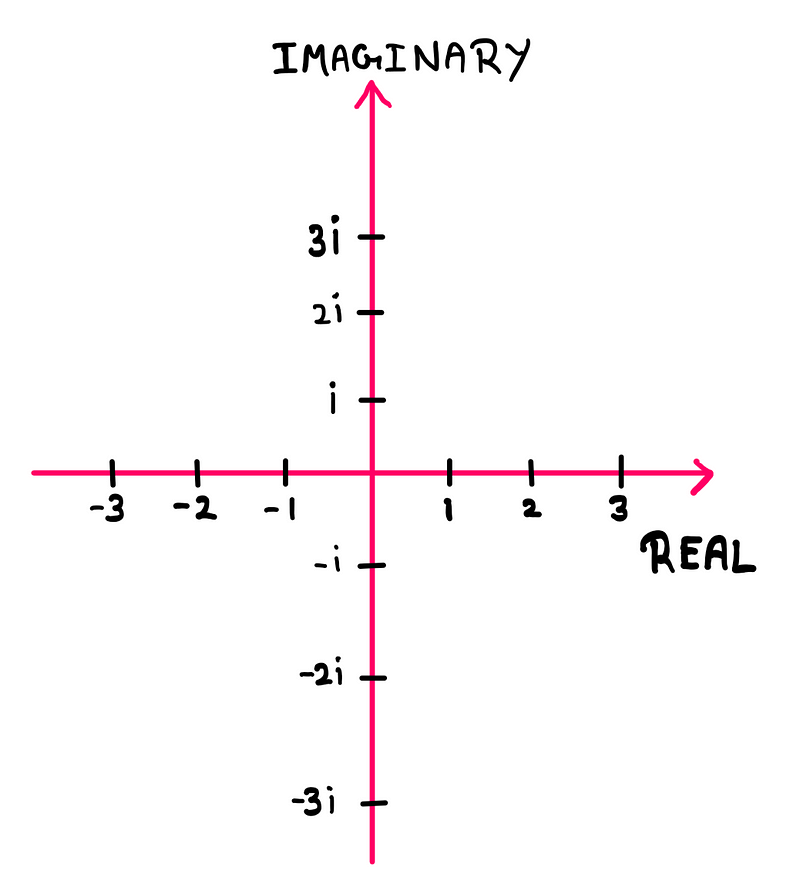
Imaginary numbers become particularly useful when paired with real numbers, forming complex numbers expressed in the format (x + iy). Consequently, every real number can also be represented as a complex number.

Rotating Vectors: The Key to Understanding

To grasp Euler’s identity, we can think of complex numbers as vectors originating from the complex plane’s origin. These vectors can be articulated in polar coordinates.

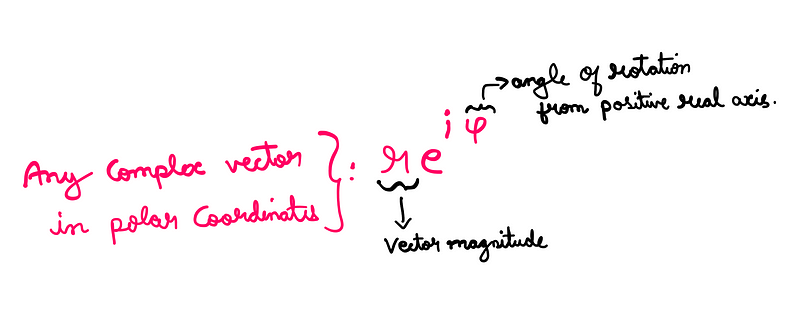
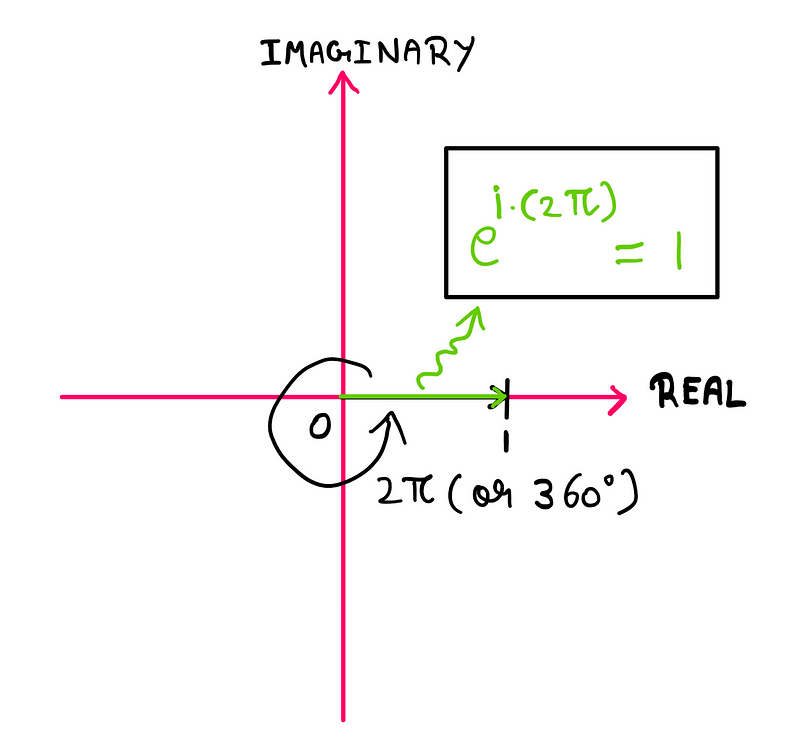
Consider a vector extending from ‘0’ to ‘1’. As it lies on the positive real axis, it initially encloses an angle of zero radians, with a magnitude of 1.

Now, if we rotate this vector by π radians (or 180°), we find it points to ‘-1’ on the negative real axis, maintaining a magnitude of 1. This can be mathematically represented as follows:

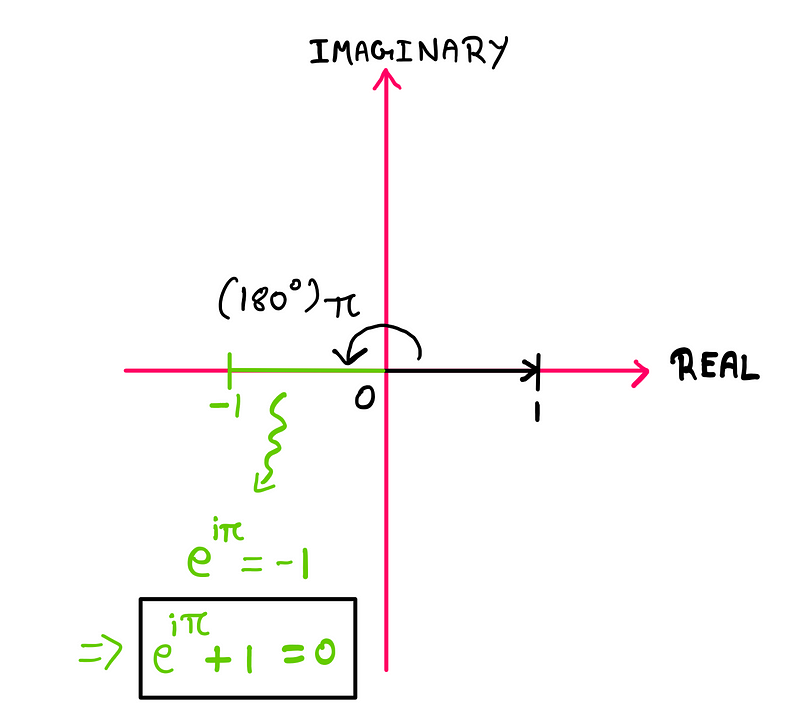
Thus, Euler’s identity conveys that rotating a unit vector along the positive real axis of the complex plane by π radians results in -1.

Similar principles apply to multiples of π. For example, rotating the unit vector by 2π radians (or 360°) brings us back to our starting point, yielding a result of 1.

Final Insights

Understanding Euler's identity can be challenging, especially when trigonometric functions are involved. This discussion aims to circumvent that complexity by focusing directly on the intuitive rotation of the unit vector along the complex plane's positive real axis.

I hope this explanation helps you appreciate the simplicity, beauty, and elegance inherent in Euler's identity. If it still feels foreign, remember that just like music and art, different individuals perceive beauty differently. It’s perfectly acceptable not to resonate with something that many find lovely.

Ultimately, a genuine appreciation for beauty and elegance should arise organically from life experiences.

If you found this article intriguing, consider supporting me by clapping, following, or subscribing!

Further reading that may pique your interest includes "Why Do We Really Use Euler’s Number For Growth?" and "What Is So Special About 69!?"

This video titled "e to the (i pi): the Most Intuitive Explanation // #SoME2 on Euler's Formula π" provides an intuitive exploration of Euler's formula.

In this video, "Intuition of Euler's Formula WITHOUT Taylor Series," viewers can gain insight into Euler's identity without the complexities of Taylor series.