Chapter 1: Introduction to Polynomials

Are you ready to master polynomials? Let’s dive into how to discover the sum and product of the roots of a polynomial.

It may seem that the polynomial presented here is quite complex. This was intentional! Instead of attempting to solve it directly—where you might find the quartic formula cumbersome—there’s a much simpler approach to tackle this conundrum. Why not give it a shot? The solution awaits below.

Let’s generalize this concept.

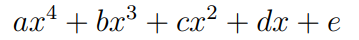
Consider an arbitrary quartic polynomial with roots labeled A, B, C, and D. This allows us to express it in a factored form:

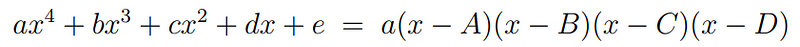
Now, let’s expand the right-hand side and extract the coefficients of each term (such as x², x³, etc.) based on the polynomial's roots. Although I’ll present the full expansion, you’ll soon realize that our focus will narrow to just a few key terms.

Prepare for an insightful journey!

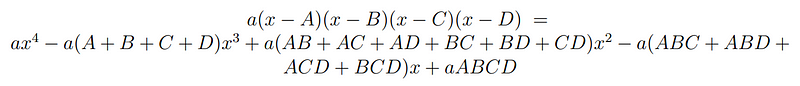
Within this expansion lies crucial information: both the product of the roots (ABCD) and their sum (A + B + C + D). Let’s filter out the excess and focus on what truly matters.

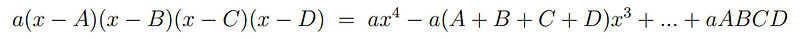
We can now reintroduce the quartic polynomial with roots A, B, C, and D.

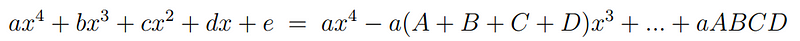
At this point, we can equate the coefficients to derive the sum and product of the roots in terms of coefficients a, b, c, d, and e. This step is pivotal, as the initial problem only provides us with the values of a, b, c, d, and e.

Let’s analyze the x³ term:

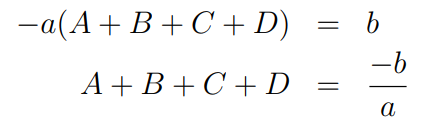
And now, the constant term:

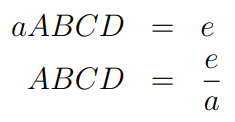
With this information, we are equipped to solve the original polynomial challenge.

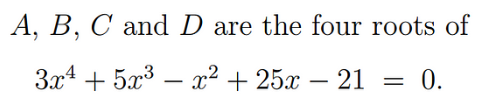
In this specific case, we have a = 3, b = 5, and e = -21, leading us to our solution.

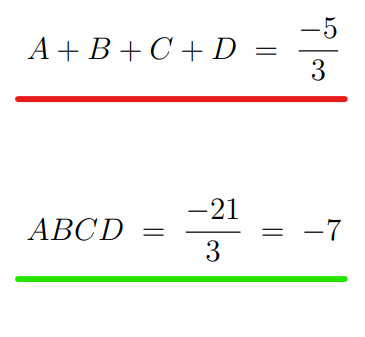
Challenge 1: Determine the sum and product of the roots for the polynomial: 2x³ - 6x² + 18.

Challenge 2: Compute the sum and product of the roots for the polynomial: 2x¹¹ - 6x¹? + 18.

Chapter 2: Video Insights on Polynomial Functions

In the first video, "Master Determining if a Function is a Polynomial or Not," viewers will learn the essential criteria for identifying polynomial functions, enhancing their understanding of algebraic concepts.

The second video titled "Algebra - MASTER Evaluating a Polynomial Function" delves into the methods of evaluating polynomial functions, providing practical insights for solving mathematical problems effectively.